Elementos de Aprendizado por Reforço
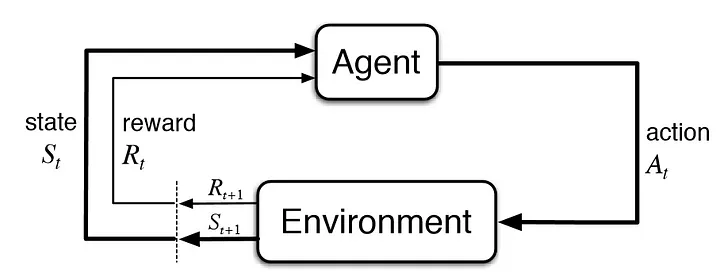
Como observado no post anterior, a idéia básica é que, a cada passo, um agente (agent) toma decisões (action) dentro de um ambiente (environment) e observa seu novo estado (state) e uma recompensa (reward). Com algoritmos corretos, podemos percorrer este ciclo diversas e diversas vezes, aprendendo quais ações nos levam a maiores recompensas e assim aprendendo a se comportar de forma inteligente dentro do ambiente.
Markov Decision Process
Em um ambiente real, passar de um estado para outro após uma ação é um processo estocástico, ou seja, existem incertezas quanto ao estado final que vamos parar. Por exemplo, temos um carro desligado (estado 1) e tentamos ligá-lo (ação): Existe uma chance alta que o carro vai ligar (passar do estado 1 para o estado 2) e existe uma pequena chance dele pifar e não ligar (passar do estado 1 para o estado 1 denovo). Em uma transição de estados sempre teremos incertezas. Para lidar com isso, em reinforcement learning, o ambiente é geralmente modelado usando um MDP ou Markov Decision Process.
graph LR
A((s0))
B((s1))
C((s2))
A -->|0.5| A
A -->|0.25| B
A -->|0.25| C
Em um MDP, dizemos que probabilidade de terminar em um estado st após uma ação a depende apenas do estado \(s_{t-1}\) e não dos anteriores (\(s_{t-2}\), \(s_{t-3}\) etc). No exemplo acima temos:
\[P(s_0 \vert s_0, a) = 0.5\] \[P(s_1 \vert s_0, a) = 0.25\] \[P(s_2 \vert s_0, a) = 0.25\]Ou seja, partindo de \(s_0\) e tomando a ação a, 50% das vezes que fizermos isso voltamos ao estado \(s_0\), 25% acabamos no estado \(s_1\) e 25% acabamos no estado \(s_2\).
Recompensas
Uma recompensa \(R(s)\) é um valor que o agente recebe por estar em um determinado estado s. Essa é a forma que um agente tem para medir sua performance no problema, do mesmo jeito que nós humanos ficamos felizes (recompensa positiva) quando fazemos algo bom, ou tristes (recompensa negativa) quando nos acontece algo ruim.
Policies
Policies são funções \(\pi(s)\) que mapeiam estados para ações, isso é nos dizer qual ação tomar em determinado estado. Em reinforcement learning, nosso objetivo é encontrar a optimal policy \(\pi*\), que é a função que vai nos dizer qual a melhor ação a tomar em qualquer estado a fim de conseguir o maior número de recompensas dentro do ambiente a partir daquele estado.
Sequencia de Recompensas e Value Functions
Vejamos o diagrama abaixo:
graph LR
A((A))
B((B))
C((C))
D((D))
E((E))
START[Estado Inicial]
END[Estado Final]
START --> A
A -->|+10| B
A -->|+100| C
B -->|-1| D
C -->|-1000| E
D --> END
E --> END
A partir do estado A, qual estado devemos ir para obter a maior recompensa, B ou C? Como ir para o estado B recebemos uma recompensa +10 e ir para o estado C recebemos +100, obviamente vamos para o estado C. Porém, olhando mais pra frente, vemos que a partir do estado C só podemos ir para o estado E e isso vai nos penalizar com -1000 de recompensa. Caso tivéssemos ido para o estado B anteriormente, só poderíamos ir para o estado D e essa penalidade seria apenas -1. Com isso percebemos que a ideia de recompensa não é suficiente para determinarmos o quão interessante é estar ou ir para determinado estado, precisamos do conceito de sequência de recompensas. Com isso podemos começar a definir nossa Value Function:
\[V^{\pi}(s) = \sum_{t=0}^{T} R(s_t) \vert s_0 = s\]Uma value function é a simplesmente a soma das recompensas R que vamos encontrar a partir do estado s seguindo a policy \(\pi\). Por exemplo, podemos dizer que a value function do estado A seguindo uma policy que escolhe o estado B é \(+10–1=9\), e da mesma forma, a value function de A seguindo uma policy que escolhe o caminho C é \(+100–1000=-900\).
Recompensas Futuras
Dada as duas sequências de recompensas:
- \[1+1+1+1+1+1+1…\]
- \[1+2+1+2+1+2+1…\]
Qual delas é a melhor? Intuitivamente diríamos a 2, já que existem alguns +2 espalhados enquanto a sequencia 1 só possui 1s. Porém ao somá-las, qual resultado obtemos? Infinito para ambas. Ou seja, embora estranho, as duas são iguais no sentido de benefício de escolha. Precisamos de uma forma de “limitar” essa soma para poder dizer qual a melhor sequência. A forma de lidar com isso é utilizar o conceito de discounted rewards, que é basicamente aplicar uma penalidade \(\gamma\) entre 0 e 1 para recompensas futuras, quão mais longe elas estão, mais penalizadas elas serão:
\[V^{\pi}(s) = \sum_{t=0}^{T} \gamma^t R(s_t) \vert s_0 = s\]Como cada estado subsequente possui também sua value function, podemos defini-la recursivamente:
\[V^{\pi}(s) = R(s) + \gamma V^{\pi}(s_{t+1}) \vert s = s_t\]Juntando tudo
Com isso, podemos juntar tudo e definir nossa value function pra valer agora:
\[V^{\pi}(s) = R(s) + \gamma \sum_{s'} P(s' \vert s, \pi(s)) V^{\pi}(s')\]Como dissemos anteriormente, uma transição de estados é um processo estocástico, então adicionamos a somatória de probabilidades de todos os proximos estados \(s’\) multiplicando suas respectivas value functions. Podemos pensar essas probabilidades como pesos: o estado \(s’\) com maior chance de ocorrer vai contribuir mais com sua value function.
Conclusão
Esses são os elementos básico de um problema envolvendo reinforcement learning. Algumas coisas foram omitidas, como provas e variações das equações, porém a idéia é dar um senso geral do que compõe um problema de aprendizado por reforço.